How To Disprove The Flat Earth

By @ScienceWasWrong

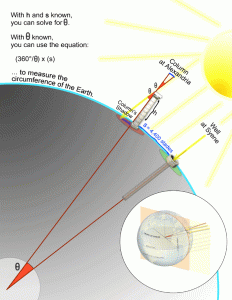
Around 240 B.C, the Greek astronomer Eratosthenes devised a way to measure the circumference of the earth. He knew that each year on the summer solstice the sun would pass directly overhead and illuminate the bottom of a well in the city of Syene, about 500 miles south of Alexandria on the Tropic of Cancer. On that day, when the sun was at its highest in the south, he found that a stick in Alexandria cast a shadow at a 7.2 degree angle. This angle corresponds to the solar zenith angle – the angle between the sun and the point in the sky directly overhead. He reasoned that the distance between the two cities must therefore constitute 7.2 degrees of a circle, which indicates a circumference of about 25,000 miles.

Eratosthenes made two assumptions here: that the earth is a globe and that the sun is distant enough that its rays are essentially parallel.  Eratosthenes’ experiment alone does not prove that the earth is a globe because his assumptions must be true in order for his conclusions to be valid. Flat earthers reject these assumptions and posit that the sun is much smaller and closer to the earth so that its rays are not parallel. This can produce a 7.2 degree shadow just as easily. In order to find out which is the case, we must work backwards from these assumptions and see what each would entail if true, then we can find a way to test them.

After arriving at the circumference of the Earth, Eratosthenes is said to have made an ambitious attempt to map it. In doing so, he helped to invent the concept of latitude and longitude, a geographic coordinate system based on angular distance north or south of the equator and east and west of the prime meridian. In order to find the latitude of Alexandria, Eratosthenes would have just needed to wait until the winter solstice and repeat the experiment, in which case he would have measured a shadow angle of 56.2 degrees. Subtracting the 7.2 degrees between Alexandria and the Tropic of Cancer, this gives 48 degrees as the angle between the Tropic of Cancer and the Tropic of Capricorn. Dividing by 2, this would have placed the Tropic of Cancer at 24 degrees north of the equator (the latitude of the Tropics have fluctuated throughout history and continue to do so today) and Alexandria at 31.2 degrees north.

Modern science places the earth’s radius at 3,959 miles, which gives a pole to pole circumference of about 24,875 miles. Dividing by 360, we find that one degree of arc should be about 69.1 miles on the earth’s surface. That is why lines of latitude are about 69.1 apart. So on a globe for every 69.1 miles or one degree of latitude you move north or south of the point the sun is directly overhead, the angle of the shadow in that location would increase by one degree. If Eratosthenes was correct, the angle of his shadow must have been equal to Alexandria’s latitude north of Syene, because that would be the angle that Alexandria is leaning away from Syene due to the curvature of the earth. If three other astronomers had performed the experiment on the same day at 20 degrees, 40 degrees, and 60 degrees north of the Tropic of Cancer, they would each respectively measure a shadow angle of 20 degrees, 40 degrees, and 60 degrees, and all would arrive at a circumference of 24,875 miles. The beauty of Eratosthenes’ experiment is that you can repeat it anywhere on earth, on any day of the year, and arrive at the same circumference. This is where the flat earth model runs into problems.

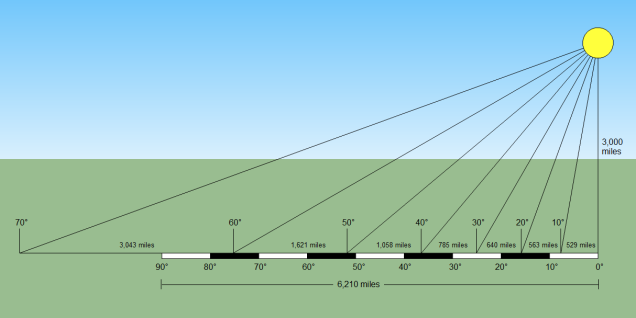
In the flat earth model, as a consequence of geometry, as your distance from the point the sun is directly overhead increases, the distance between each successive degree of shadow will also increase exponentially. For example, assume the sun is giving off a 45 degree shadow at 45 degrees north, as depicted in this flat earther meme. If the earth were flat, that would mean that the sun is, more precisely, 3,110 miles high. In that case, it would be 1,132 miles to the 20 degree shadow, 1,478 miles between the 20 and 40 degree shadows, and a whopping 2,777 miles between the 40 and 60 degree shadows. Someone performing Eratosthenes’ experiment at 20 degrees north of the Tropic of Cancer would arrive at a circumference of 20,376 miles, someone at 40 degrees north would get 23,486 miles, and someone at 60 degrees north would get 32,320 miles.

Flat earthers use the Azimuthal Equidistant Projection map, which shows all points at an undistorted distance and direction from the center. Lines of latitude on the flat earth map have the same spacing as those on the globe: 69.1 miles per degree. It is for this reason that the angle of the shadow can only be equal to the degrees of latitude between you and the point the sun is directly overhead in one location. Everywhere south of that point the shadow angle would be greater than the latitude and everywhere north of that point the shadow angle would be less than the latitude. If the sun were 3,110 miles above the flat earth, the 20 degree shadow would be 16.4 degrees north, the 40 degree shadow 37.8 degrees north, and the 60 degree shadow 78 degrees north. Only at 45 degrees north would the latitude and the angle of the shadow actually match as they would everywhere on the globe and only there would someone arrive at a circumference of 24,875 miles. You can change the height of the sun all you like, the latitude and angle will only be the same in one location. Even then, it is only a coincidence due to the random height of the sun, not a direct function of latitude as it is on the globe.

To be sure, if each of our astronomers were to measure a shadow angle corresponding to their latitude, as is to be expected on the globe, and you were still assuming a flat earth model, that would require that from 20 degrees north the sun be 3,797 miles high above the flat earth, at 40 degrees north 3,294 miles high, and at 60 degrees north 2,393 miles high. An impossibility. The only possible solution would be to distort the flat earth map beyond recognition by staggering the lines of latitude, but even then it would only be correct for a single day, as the sun moves to a different latitude each day and the model would again become increasingly wrong.

So to recap, if the earth is a globe, the angle between the sun and 90 degrees overhead must be equal to the degrees of latitude between you and the point the sun is 90 degrees overhead in every location. If the earth is flat, this can only be true in one location. Testing this discrepancy between these two models has the potential to end to this debate once and for all.

You can do this test yourself. You can’t be in two places at once to take multiple measurements on the same day but, lucky for us, the zenith angle of the sun in the sky changes everyday as the sun moves between the Tropic of Cancer and the Tropic of Capricorn. Since the sun is moving a fraction of a degree north or south each day, you can stay right where you are and test a new angle every day.

1. Go to this website, enter your location, and look at the sun transit time to find out when the sun will cross over your line of longitude, when it is directly south of you.
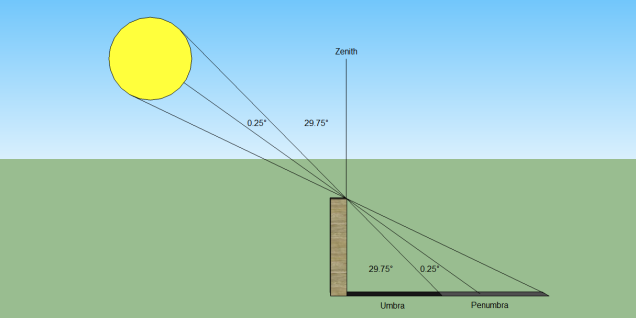
2. When this time comes, go outside, find something that casts a shadow, measure it, and carefully measure the length of the shadow. Only measure to the edge of the solid dark part of the shadow, not the lighter penumbra at the end.
3. Divide the length of the shadow by the height of the object and hit inverse tangent on your calculator to get the angle of the shadow. For precision’s sake, the sun has an angular diameter of about 0.5 degrees. The end of the dark part of the shadow is defined by light from the top of the sun passing over the top of the object, while light from the bottom of the sun crosses over the top of the object to mark the end of the penumbra, giving it the same angular width as the sun. To get the zenith angle of the center of the sun, add 0.25 degrees to your shadow angle.
4. Go to this website and see which latitude the sun was overhead at the time you measured the shadow.
5. If the sun is in your hemisphere and at a lower latitude, add the sun’s latitude to the angle you measured. If it is in the same hemisphere and at a higher latitude, subtract the angle from the sun’s latitude. If it is in the opposite hemisphere, subtract the sun’s latitude from the angle you measured. First convert the latitudes’ arc minutes to decimals by dividing by 60. (Example: 46° 34′ = 46 + 34/60 = 46.567°)
6. If the earth is a globe, the result, depending on the precision of your measurements, should be equal to your latitude.
7. To find the circumference of the earth as Eratosthenes did, multiply the shadow angle by 69.1 miles to get the distance. Divide 360 by the angle of the shadow, and multiply that by the distance. If the earth is round, the result should be close to 24,875 miles.

Alternatively:

1. Find the angle of a shadow at ANY time of day when the sun is out.
2. Find out where the sun was at overhead at that time.
3. Type those coordinates into Google Earth and measure the distance from there to your location with the ruler set to degrees.
4. Compare this to the angle you measured.

This method is especially damning because of the degree at which longitude lines diverge south of the equator on the flat earth map.

Still unconvinced by the astronomical coincidence that at a random time on a random day the sun was at the correct height and distance to be at the same angle in the sky as your random latitude north or south of it? Well it’s the moment of truth, because the angle should get progressively wronger with each passing day. Try it again the next day, or the next day, or the day after that. You can also do this:

1. Multiply the angle by 69.1 to get your distance from the point the sun was directly overhead.
2. Divide this by the tangent of the angle to get what should be the height of the sun if the earth is flat.
3. Now see what latitude the sun will be overhead two weeks from now. Convert it to decimals. If it’s in the opposite hemisphere, add it to your latitude, if not, subtract the lower from the higher. This is the angle of the shadow you should get if the earth is round.
4. Multiply this angle by 69.1 to get the distance.
5. Divide the distance by the height of the sun from step 2 and hit inverse tangent to get the angle of the shadow you would expect on a flat earth.
6. Wait two weeks and find the angle of a shadow again as you did in the first test.

If you get the angle you found in step 3, the earth is round. If you get the angle you found in step 5, the earth is flat. Still not convinced? Try it on the winter solstice, the spring equinox, and the summer solstice. Be amazed as you get the same angle you would expect to get on a globe each time.

Is there any way for a flat earther to ad hoc their way out of this? They could say that the sun is constantly changing height to give you the correct angle. Presumably it would be doing this for your sake as it would only work for someone at your exact latitude, giving everyone else in the world wildly inaccurate results. They could say the sun position website is wrong and the sun is moving away at increments that give you the correct angle each day, even though again, this would only be working for you. If you’re in England, the sun would have to be past the ice wall on the winter solstice to get an angle like 75°. They could come up with some kind of woo about the position of the sun being an illusion, but while you’re over there in David Copperfield land with your buoyancy gravity, we’ll be here in reality getting things done.

 

The UNI-VERSE Meme™

by @SuckItEvolution with @TkThtEtymology

There’s a pernicious and annoying little theist meme that’s been spread all over Twitter and other social media channels for several years now. Every so often, you’ll see it getting re-cycled and re-tweeted by new enthusiasts encountering it for the first time. I like to call it “The UNI-VERSE Meme”. It has a number of popular variations, but basically goes something like this (caution: you might want to have a good, stiff drink, before reading further):

“UNI” = One, or single;
“VERSE” = Spoken (or occasionally written) word, phrase,\\ or sentence;
“UNI-VERSE” = A single, spoken word or sentence;
→ Our universe is a “UNI-VERSE” — Created by a single spoken WORD or SENTENCE, uttered by God!

UNI-VERSE meme fans are not quite decided on whether “UNI-VERSE” means a single word, sentence, or phrase (hence, my canonical rendering above). But no matter — they press on undeterred! Often, they’ll embellish the meme with their own creative nuances. Some even seem to suggest that our physical universe IS that single word or phrase, suspended in the aether like some grand Platonic archetype. Here are just a few examples I’ve harvested from Twitter (note: I’ve posted these as simple screen captures, because the embedded tweets were simply taking too long to load):

Yes, wake up:

Oh, I’ve definitely thought about it:

Adam gets it, of course. Too bad nobody else does:

Sometimes, they don’t really bother to elaborate on what their point is. The meme has become so embedded that they simply repeat it without even giving the punchline. Like The Monkey Question, it is a shibboleth of creationist nonsense.

Now, what I find so exasperating about this meme (and I’m sure many of you do, as well) is that it is not based on the actual meaning, or origin, of the term universe, as used by most English speaking people today. Not in the least. Consider, for example, the English Wikipedia page for Universe, which traces this word’s etymology as follows:

The word universe derives from the Old French word univers, which in turn derives from the Latin word universum.^[20] The Latin word was used by Cicero and later Latin authors in many of the same senses as the modern English word is used.^[21] The Latin word derives from the poetic contraction unvorsum — first used by Lucretius in Book IV (line 262) of his De rerum natura (On the Nature of Things) — which connects un, uni (the combining form of unus, or “one”) with vorsum, versum (a noun made from the perfect passive participle of vertere, meaning “something rotated, rolled, changed”).^[21]

When Googling “Universe etymology”, the first result returned to me by Google was a graphical representation of the same (more or less) above definition from Wikipedia. Following that were a number of other sources of definitions, including a link to the Online Etymology Dictionary, which defines universe as:

universe (n.) 1580s, “the whole world, cosmos, the totality of existing things,” from Old French univers (12c.), from Latin universum “all things, everybody, all people, the whole world,” noun use of neuter of adjective universus “all together, all in one, whole, entire, relating to all,” literally “turned into one,” from unus “one” (see one) +versus, past participle of vertere “to turn” (see versus).

And finally, I’d found, fairly high up there in the search results, this exquisite little gem, posted as a query to Yahoo Answers (italics added by me, to emphasize the truly sticky parts):

Atheists and the word universe?

Respectfully, do atheists have a problem with the meaning of the word “universe”? The word universe is taken from two root words….UNI meaning single… as in unicycle or unicellular and VERSE meaning sentence or spoken word. So the word UNIVERSE literally means a “single spoken word” which has connotations of God’s creative power in the Genesis acount of how God created everything by speaking it into existence. How is it that the word universe has come to mean everything in existence? or that universities are considered areas of knowledge? I’d just like to know your thoughts on this with all due respect.

Following that query were a number of replies to the contrary, most of which respectfully pointed out the error of the poster’s interpretation of the word “universe”, and generously offered more appropriate explanations, along the lines of what I’ve cited above, and with some providing links to credible sources. But this thread was finally capped-off by one last reply, from yet another meme enthusiast whom I guess just wasn’t satisfied with the more thoughtful responses, and felt it appropriate to come to the rescue by reiterating the basic canon:

Uni=One
Verse=spoken phrase
Universe=One spoken phrase
As in “Let there be”

So, … why does this silly Twitter meme stick so badly in my craw that I simply can’t ignore it? I suppose there are many reasons; here are the three main ones:

1) The meme is completely incorrect and intellectually dishonest. While it’s uncertain if he was the ultimate originator, Kent Hovind was responsible for the initial popularity of this meme, and as usual you can bet that, immediately after its conception, its progenitor didn’t think even once about looking up the true etymology of “universe”, which, as I’d demonstrated above, is but a few clicks away. Either that, or he dismissed the actual accounts as academic-liberal rubbish. There is, of course, a third possibility — that of a charlatan or troll deliberately releasing the UNI-VERSE meme on the gullible, assured it’d eventually spread like the insidious virus it is, and certainly succeeding in the end. But in any event, new adopters of the meme certainly don’t bother checking whether what’s being claimed is real, or not. I doubt they care.

2) Spreading the meme doesn’t make it so. This seems like a real problem with the present-day crop of theists and conservative wing-nuts: No matter how many times they tweet and re-tweet this lame-ass claim of the meaning of the word “universe”, they’re not going to somehow make it true. And they’re certainly not going to make true the vague and sloppily conceived idea it represents. It’s just like claiming “God is real because, after all, we always spell ‘God’ with a capital ‘G’, don’t we?” But these folks invariably get totally caught up in all this silly word play, while deliberately ignoring the factual and substantive.

3) Which “Single Word” or “Single Phrase” are you talking about, anyway? The Book of Genesis of the Hebrew Bible describes God as uttering many incantations, which, over the course of six days, collectively brought earth and heaven into full being. Many “single phrases” were spoken, not just one. Furthermore, there’s no account of God actually creating anything like the universe, as we know it today. God essentially formed heaven and earth by forcing asunder the surrounding “waters of chaos”, and inserting a firmament to keep separate the “waters above” from the “waters below”. But God isn’t claimed to have created the waters prior to dividing them. Nor the land that appeared once the waters were separated. Were the “waters of chaos” believed to be eternal by ancient people? Possibly. But unfortunately, the UNI-VERSE meme fans seem so absorbed in their shared delirium, they’ve even lost sight of the literal account of their own creation myth.

4)As with a lot of language-related mysticism I see, in addition to being a completely incorrect meme, the projection that the etymology of the word somehow reveals a secret about what the denoted object or idea truly means is a bizarre non-sequitur. As noted above, very literally, the primitive roots of “universe” would best be translated “turned into one”. It is still equally bizarre to make a claim that this proves that there were once many things that were separated which have now become one. The argument by etymology, with or without a correct etymology, is a case of the Genetic Fallacy.

5)Even if the etymology were correct, the meme would require that the mystical power imbued into the word which reveals the true nature of reality exist only in the languages which share the root for this particular concept with English. The literal etymology (or in some cases, the literal meaning) of the word for “universe” in other languages include such things as “order”, “all worlds”, “world in general”, and “wholly everything”. As I often like to joke, if we imbue the same mystical properties into the Dutch word for universe, “Heelal”, literally “wholly everything”, then we have proven that physical existence is all there is, and thus the word proves that no transcendent god exists, since physical existence is wholly everything.

#checkmateuniverse

Presuppositional Apologetics

By @ScienceWasWrong

After realizing that they never win arguments about science against atheists, creationists have adopted a bold new strategy: making a mockery of philosophy. It was a clever choice, since some atheists seem to have the same weird contempt for philosophy that creationists have for science.

All philosophy a footnote to Plato? I’m sincerely curious why Plato is so revered. What was he actually right about? I’m honestly ignorant.

— Richard Dawkins (@RichardDawkins) March 22, 2015

Presuppositional apologetics is the bastard child of this unholy union between creationists and philosophy. Since the facts aren’t exactly on the creationists’ side, they’ve decided that facts are irrelevant because people only interpret facts according to their worldview. Since atheists apparently presuppose that God doesn’t exist, it’s not at all circular for them to presuppose that God does exist. With those mental gymnastics out of the way, they’ve made an attempt to create a monopoly on the existence of facts. The basic argument behind presuppositional apologetics is this:

1. If God did not exist, knowledge would not be possible.
2. Knowledge is possible
3. Therefore God exists

Earth shattering, I know. With this, they can avoid actually refuting arguments and just ask “why?” like a 3 year old to everything their opponent says before scolding them for making unsubstantiated knowledge claims. Unsurprisingly, Eric Hovind has become a major proponent of this line of argument, either to distance himself from his father’s “contributions” to science, or simply because all that sciencey stuff is over his head. Hovind’s approach goes like this:

1. Could you be wrong about everything you claim to know?
2. If you could be wrong about something, then you don’t really know it.
3. You can’t know anything unless you know everything.
4. The only way for us to know anything is for someone who knows everything to reveal it to us.

Number 1 is self defeating because if it’s possible for you to be wrong about everything you claim to know, then admitting that would make you correct about something. Number 3 is inconsistent with itself, because not knowing everything is the pre-condition for knowing that you don’t know everything. Number 3 and 4 are contradictory. If you can’t know anything without knowing everything, then you can’t know whether someone who knows everything has actually revealed anything to you or if you’re just deluded. A twelve year old has pointed this out to Eric.The argument collapses entirely if it is asked whether you could know number 4 if God did not exist.

The Ray Comfort to Eric Hovind’s Kirk Cameron is a former boiler room employee named Sye Ten Bruggencate. Sye has achieved notoriety for his website http://www.proofthatgodexists.org in which you are coerced into clicking criminally unnuanced answers to a series of questions about absolute knowledge and logic which have nothing to do with the subject at hand. Sye’s style is similar to Eric’s, albeit even more intentionally confusing. His approach revolves around the question “how do you know your reasoning is valid?” You can’t use reasoning to justify your reasoning because that would be “viciously circular.” His thesis is that the only way for us to be “absolutely certain” we are not a brain in a vat is through divine revelation.

He also debated Matt Dillahunty one time and actually opened this syllogism:

1. It is reasonable to believe that which is true.
2. It is true that God exists.
3. Therefore it is reasonable to believe that God exists.

A line of argument which, I shit you not, he calls “virtuously circular.”

It turns out that you can use reasoning to justify your reasoning because, by Sye’s own terms, someone with invalid reasoning would not be capable of recognizing that their reasoning is invalid. So simply acknowledging the possibility that your reasoning is not valid entails that it is valid. Regardless, his idea that divine revelation can validate his reasoning is simply something his reasoning has told him. That you can be absolutely certain you’re not a brain in a vat in this way assumes a brain in vat could not be fooled into thinking it has received a divine revelation. What it boils down to is that he “knows” he is not a brain in a vat because he believes he is not a brain in a vat. If you trust your senses enough to read the Bible, then you’ve already made the assumption that the world around you is real and you don’t really need the Bible’s contents to prove it.

Oh yeah, and all of these arguments are rendered meaningless by the primacy of existence axiom, which says the universe exists independently of consciousness. So there’s that.

It’s Just Not NATURAL, Damnit!!!

Or… “The Inigo Montoya Fallacy”

by @TakeThatHomo

One of the most popular attempts at a non-religious argument against homosexuality is the Appeal to Nature, or the Naturalistic Fallacy. It’s one of those arguments that make me roll my eyes and shake my head. I try, most of the time, not to judge any of the people who argue against the gay community, be it on the basis of marriage or just in general, because they genuinely believe that they are right. People hold their opinions for a reason, be it religious or logical (at least to them), so when I come across Tweets like this:

https://twitter.com/M0RNiNGW00dY/status/598897506785734656

https://twitter.com/ebonymacarthy/status/598878801737719808

It is easy to reply with something like “homosexuality occurs in nature, therefore is “natural”. You’re welcome.” By the time I find these Tweets someone else has usually got in there before me with some variation of the rebuttal, like pointing out how many different species engage in homosexual acts in the natural world. From the point of view of the liberal, equal opportunities Tweeter this is the end of the argument. Someone has made a statement, and that statement has been shown to be incorrect. How can the argument continue?

Oh, how naive of us to believe that this is the case. The individual making the statement can simply ignore the facts and just keep repeating the claim, even when you pull up links to scientific papers on the subject or the actual definition of “natural”, which can be beyond frustrating. In these cases there really is no point in continuing with the conversation. If someone refuses to concede to a scientifically proven fact then there’s not really anywhere you can go.

The alternate route will quickly transform the argument from the appeal to nature to the religious argument, which is much more interesting but harder to keep on track. That’s something that I will cover at another time, because there is something that is frequently missed when it comes to the “it just ain’t natural” claim.

When the wingnuts use the word “natural” they’re not using it in the way that we are. It’s the homophobic version of “evolution is just a theory” that my esteemed colleagues @TakeThatDarwin and @TheoryFail have to deal with. Those people are using “theory” to mean “guess” or “idea” or “hunch”, rather than the actual context in which it is meant; that of a scientific theory (which I’m not going to cover because that’s best left to people who know what they’re talking about).

What the homophobe is doing in this situation is making a moral judgement about what the word means, and they’re getting it wrong. What they’re doing here is equating “natural” with “good” or “right”. They don’t like the idea of homosexuality. Most of the wingnuts on Twitter that I find have a particular vehemence towards man on man action. They find it disgusting and can’t get their brains around why any real man would want to do that sort of thing with another male. It makes them uncomfortable to see same sex affection, they don’t like seeing gay characters on the television or in the movies and it makes them feel icky. This is because it is outside of their normal experience. Twenty years ago the same could be said of mixed race relationships. They weren’t exposed to such relationships and therefore judged them as unnatural, or bad, or wrong.

In the minds of these people good equals natural, so because homosexuality is not good then it must be unnatural. How could it be anything else? This is the root of their argument in most cases. When someone uses the “homosexuality is not natural” argument they are begging the question, because they are already putting their conclusion in their premise.

Nature, however, doesn’t make implicit value judgements. There is no “good” or “bad” or “sin” in nature, there is just “nature”. To assert that natural equates good means that accepting rape is good. Rape occurs in the natural world, therefore rape is good. A lion taking down a gazelle is natural, therefore murder is good. Cancer is natural, therefore disease is good.

This is the true meaning of what they think “natural” means. As usual it is religious indoctrination that leads to this conclusion. Homosexuality is going against the plan of God, and therefore not natural. The fact that it is present in thousands of species is irrelevant to them. It’s nothing more than an attempt to frame their religious world view in a secular standpoint.

When you hear the argument that homosexuality is not natural perhaps it might be an idea to find out what they think “natural” means, because if you leap into a defence of what you think they mean you may be coming at it from the wrong angle.

Thank you for reading, please leave a comment and if you have any ideas for future posts then please leave a comment or contact @TakeThisBlog.

The Kalam Cosmological Argument

By @ScienceWasWrong

1. Everything that begins to exist has a cause.
2. The universe began to exist.
3. Therefore the universe had a cause.

(P.S. the cause is God.)

This argument is disarmingly simple. It is intuitive, seemingly reasonable, and a person doesn’t have to go against the entire scientific establishment to make it. However, it is only simple out of necessity, for the differences between our understanding of causality and the conditions at the beginning of the universe will soon make themselves apparent.

Epicureanism taught that the universe is made up of a finite number of indestructible atoms that move around in a void. Things only come into being through the atoms forming new compounds after atoms from old compounds are broken apart and recycled. This was an early description of the first law of thermodynamics. Nothing is ever created from nothing, cause or no cause. Everything is just different arrangements of atoms that have existed since the beginning of time. Already you can detect a false equivocation here of the way things made of matter begin to exist and the way matter itself begins to exist.

The argument claims that everything which begins to exist has a cause, but in reality everything that begins to exist has several causes. Aristotle posited four types of causes:

1. Material cause – The material that is caused to become something.
2. Formal cause – The form that the material is caused to take.
3. Efficient cause – The thing that does the causing.
4. Final cause – The reason for the cause.

For example: A carpenter (the efficient cause) assembles pieces of wood (the material cause) into a table (the formal cause) so he can sell it to a customer (the final cause). The carpenter does not literally cause the table to exist (you can not cause something that does not exist to do anything) rather he causes material that was not the table to become the table. This is why everything which begins to exist through an efficient cause also has a material cause.

What can this tell us about the beginning of the universe? Christian theology is adamant that God created the universe ex nihilo – out of nothing. There could not have been a material cause for the universe because if any material existed before the universe, it would already have been defined as the universe, which would mean that the universe did not begin to exist at all. The universe could only have had an efficient cause, which the argument suggests is God. But if there was no material cause, then what did God causally affect when he created the universe? It couldn’t have been the universe because the universe didn’t exist yet. Did he act on nothing at all and the universe just popped into existence? An affectless effect? In what sense does that qualify as a cause? It’s not absurd, it’s incoherent. The only option that even begins to conform to our understanding of causality is creatio ex deo, the idea that God caused himself to become the universe. If not that, then the type of cause that created the universe was so far removed from our understanding of causality that the universe might as well have just had an a-causal beginning.

Credit for much of this argument goes to @CliftonsNotes aka Theoretical Bullshit aka Liam from The Bold and the Beautiful. His series of videos on the Kalam argument and hilarious interaction with William Lane Craig can be found here.

The Moral Argument

By @ScienceWasWrong

The moral argument for God’s existence, as formulated by professional philosopher William Lane Craig goes like this:

1. If God does not exist, objective moral values and duties do not exist.
2. Objective moral values and duties do exist
3. Therefore God exists

It is important to ask exactly how objective moral values exist if God exists. People who make this argument usually subscribe to a divine command theory of ethics, which asserts that what is moral is determined by what God commands, and that to be moral is to follow his commands. Socrates discovered the most glaring flaw in this system when he asked Euthyphro: “is the pious loved by the gods because it is pious, or is it pious because it is loved by the gods?” Is something good because God commands it, or does God command it because it is good? If it is the former, then that makes makes morality arbitrary. God could command genocide and it would still be considered good because he commanded it. If it is the latter, then that makes morality independent of God. God would simply be the middle man in informing us of what is good.

After much deliberation, apologists have decided that the answer is actually neither: God commands something because he is good. Goodness is rooted in his nature, which is reflected in the goodness of his commands. This gets rid of the dilemma momentarily and usually gets people to stop asking questions, but it has serious consequences in that it entirely strips goodness of any meaning. If to be good simply means to be like God, then when you say God is good, all you are saying is that he is like himself. It then becomes inexplicable why God has the properties that he has rather than other properties. If God’s nature were one of dishonesty for example, then he would command dishonesty and dishonesty would be considered good. Theists will outright deny this, but the fact that they deny it shows that there must be more to something being good than it being part of God’s nature.

It’s like saying Abraham Lincoln is the standard for tallness. If this were true, then to be tall would mean to be similar in height to Abraham Lincoln. If you accept this, you must also accept that if Abraham Lincoln were only 3 feet tall, then that is what we would consider tall. If not, then Abraham Lincoln was never actually the standard of tallness, the standard was his relative distance above the ground. Unless goodness is defined in some quantifiable way, such as that which promotes well being, then it becomes arbitrary. It might be complained that this definition is simply my opinion and therefore arbitrary as well. Well, if morality is not intended to promote well being, then what exactly is the point?

What About Whataboutism?

By @TakeThatHomo

We’ve all been there. We’ve seen it happen. You’ll be happily pointing out the errors in someone’s argument or having a general debate on whether George Lucas should be flayed for making the Star Wars prequels when your opposition trots out a time honoured tactic for diverting the subject. You’ll be making valid points, whilst possibly adding them to some convoluted scoring system that you’ve created in your head until you reach the point when you’ve “won”, when they pull out the “whatabout” card.

Let’s say you’re discussing one of my favourite topics: equality for homosexuals. Last month I had the joy of retweeting wingnuts who had a biblical perspective on a dinky little place called Memories Pizza, who stated that they would refuse to cater for a same sex marriage. No one asked them to, but they felt the need to make their stand regardless. Personally I think a marriage with pizza provided would be all kinds of awesome, but that’s beside the point.

So you’re cheerfully pointing out that yes, businesses have to abide by the law even when it comes to something as stupid as catering pizza when they throw “yeah, but what about ISIS throwing gays off buildings in Syria” at you. This is a whataboutism and you need to avoid it at your peril.

The technical term for a whataboutism is the Fallacy of Relative Privation, which is used in an attempt to try and dismiss your argument. Sure, things might not be good for the queers in America, but they’re not getting hurled from buildings. Okay, so misogyny is bad, but women aren’t even allowed to drive in Saudi Arabia. There are children starving in Africa!

It’s an attempt to make you falter and if they whip that bad boy out you’re probably using good tactics. One subject has nothing to do with the other. The fact that ISIS have thrown people from buildings simply for suspected homosexuality has nothing to do with the catering concerns of Christians in California (yes, I know the pizza place was in Indiana, but I like alliteration).

You are actually allowed to be opposed to multiple things at the same time. People being stoned to death or thrown off buildings does not invalidate your argument. It does not make misogyny the lesser of two evils and therefore acceptable. The fact that there are starving children in the world is a horrible thing that should be ended, but has nothing to do with whatever you’re opposing.

A whataboutism is nothing more than an attempt to divert the topic, to shift it by saying “that’s bad, but this is worse” and in no way invalidates your argument. If you volunteer at an animal sanctuary your actions aren’t invalidated by the fact that people are sleeping on the streets. It doesn’t mean that you approve of the latter because you support the former.

Beware of the whataboutism, learn to spot it and cut it out of the conversation as quickly as you can, or you’ll just end up trying to justify your position as worthy when it doesn’t need to be.

The Gay Marriage “Debate”

By @TakeThatHomo

Most of my retweets come via America, since the only basis for opposing homosexuality (that I have found) comes from a religious viewpoint. Despite being founded on a secular ideal, the land of the free and the home of the brave is ridiculously religious, which is particularly strange for me since I come from a Christian country that has a fairly secular society.

Recently, however, there has been an upsurge of anti-gay tweets from a little closer to home.

There will shortly be a referendum on changes to the Constitution of Ireland, which has got a fair few people in a bit of a rage for some reason. At the time of writing seventeen countries perform same sex marriages, and the world has yet to be destroyed. There haven’t been any floods sent, nor cities toppled by earthquakes. Miraculously our little planet has yet to be demolished by an asteroid despite the fact that two people of the same sex can get married.

Whilst the religious argument against homosexuality can be fun to debate, it doesn’t really work in reasoned discourse. Theists might cling to their Bibles and recite verses that agree with their position, but it’s a little too easy to tie them up in knots, although it’s entertaining to watch them squirm and twist in an attempt to justify things like slavery and rape. The referendum has split a devoutly religious country, with #VoteYES and #VoteNO both using biblical scripture to promote their choice.

There is, however, a number of people attempting to avoid using Christianity as a reason to cast a negative vote. They’re attempting to use a scientific argument that they genuinely believe works, and they’ll keep using it even after it’s been demonstrated to them that it is wrong.

I’ve recently been retweeting @pauljoneill, who first brought this “argument” to my attention, or at least made me care enough to respond. He stand against same sex marriage because… wait for it… gay people can’t have children and therefore should not be able to get married.

https://twitter.com/pauljoneill/status/595578534942355456

As is customary with TakeThat accounts, we have followers who let us do the work of finding these wingnuts and then engaging them in discussion. Some are polite and civil whilst others simply abuse them. I prefer the former when I engage in discussion as calling someone names is rarely likely to get them to change their minds. What I noticed in the replies to Mr. O’Neill was that a lot of people were using the wrong argument to illustrate that he was incorrect in his opinion.

The general tactic that I saw was examples of other people who can’t procreate and, by his rule, should not be allowed to get married. So there were lots of “what about infertile couples?” or “then the elderly should not be allowed to get married” and “I have no intention of having children, is my marriage false?”. Whilst these statements are entirely correct, they’re missing the point.

The first half of @pauljoneill’s argument is truthful, once he made the amendment of “naturally”. At this point in time two gay men or two gay women cannot produce a child without intervention. This could be surrogacy or adoption, but these are not “natural” means. There is nothing wrong with the first half of this statement, but it has nothing to do with the second half.

According to Google, marriage is “the legally or formally recognized union of a man and a woman (or, in some jurisdictions, two people of the same sex) as partners in a relationship”. Dictionary.com has an entire list of examples of what a marriage is and do you know what is missing? Children. There is no part of the union of marriage that requires there to be children involved.

Other tweeters opposing same sex marriage have attempted to use the same argument: Two people of the same sex cannot produce offspring naturally so should not be allowed to marry. Rather than start a debate with examples of others who cannot procreate I have found it is better (and quicker) to point out that marriage has nothing to do with procreation, and procreation has nothing to do with marriage. Marriage is nothing more than a legal contract between two people and the tactic of linking it with procreation is fallacious.

Once this is pointed out to them they inevitably take a step back and bring in the Bible, which is where the fun can really start.

I bring this up because it’s important for those of us who engage people on Twitter, who seek out others who have different views from ourselves, to remember to stick to the topic.  Don’t allow them to shift it to something else. Evolution is not about the origin of life. Marriage is not about procreation. Just because you don’t know the origin of the universe does not make science defunct. It’s an attempt to move the argument into an arena that they think they can win. Look at what they’re saying. Does it make sense or can you erase it in 140 characters or less?

A Change of Kinds

By @ScienceWasWrong

Ray Comfort once ventured to a mysterious pagan temple known only as a university with one goal in mind: like Darth Vader searching for the stolen plans, he would stick his microphone in the face of every sentient creature there until one of them gave him observable evidence of a change of kinds. When no one had any idea what he was talking about, he declared that the jig was up and evolution had finally been debunked. Ever since that day, creationists have continued to run this argument into the ground and no one still has any idea what they are talking about. The go to response is “well, what is a kind?” A valid question, but the creationist will inevitably spike the football and chide the stupid evolutionist for not knowing what a cat is, or something equally vague. What is a kind you ask? It is the most diabolical thing ever conceived by a creationist. William Jennings Bryan is probably in his grave right now smacking himself for not coming up with this shit. No one seems to be able to articulate what is wrong with the argument because there is nothing wrong with it. They have actually taken the way evolution is supposed to work and used it as an argument against evolution.

The first definition of a kind is a group of animals that they are willing to admit share common ancestry. This definition alone makes it something that cannot possibly change. Sometimes they say it is more at the family level of classification. In evolution, a family is nothing more than a group of animals who share a set of characteristics they inherited from a common ancestor who also had those characteristics. If a turtle evolves into a giraffe for some reason, it would still be a part of the turtle family, the only thing that has changed is what it means to be a turtle has become less specific because the family has become more diverse. There’s already a concept in taxonomy that describes this: it’s called a monophyletic group. Over the course of evolution, nothing ever leaves the groups that their ancestors were a part of. They only form new subgroups as the old groups become more and more diverse. It’s like Russian nesting dolls.

The second definition of a kind is a group of animals that look so much alike that not even creationists can deny they are related. This is because evolution happens one change at a time. Animals with a more recent common ancestor will have more in common because there has been less time for changes to accumulate between them. Animals with a more distant common ancestor will have less in common. That’s the entire basis of what Darwin was getting at, yet that’s where they’ve gotten the idea of micro-evolution and that’s where they’ve gotten the idea of kinds. In order to prove evolution, they demand to see less in common from animals that share a more recent common ancestor, the exact opposite of what evolution predicts. That’s where Ray’s sneaky request for observable evidence comes into play. Since you can’t observe when a group of animals has a more distant common ancestor, it falls into the realm of historical science and is thus on equal ground with the science of iron age tribal poetry.

You can try to explain all of this to creationists if you want, but they will probably just tell you to show them a fish giving birth to a monkey.

Godwinning

By Take THAT, Godwin!

We have all been there. Picture the following: You are having a difference of opinion with someone. Someone you deem worthy enough at that moment to actually engage regarding that subject. The discussion becomes heated and in a moment of desperation, or in an attempt to be funny, you utter the words “Yeah, well, Hitler…”

The Panic Button

Adolf Hitler represents the worst of what mankind can amount to. Everybody knows him as the ultimate personification of that universal blackness: “evil”. Funnily enough it differs from person to person what this means. If half of all accusations were even remotely true, the man would be a Leftist Right-wing, Muslim atheistic Reptilian Alien with a surprisingly mundane warm streak. The invocation of Hitler has very little to do with an actual argument. It is an appeal to emotions; a fallacy directly opposite to the reason we all stand for.

In the early days, when Take That Darwin was the first and only #TTCOT-account, I was surprised at the amount of stoopid the world could produce. Being a Christian in rehab, I started following all of the (now famous) retweets of Christians to be reminded of some of the darker sides of my former faith, but what I was offered was usually the more dimwitted side. However, after while I noticed that both sides of the argument were very quick to prove Godwin’s Law right.

Godwin’s law states – and I quote: “As an online discussion grows longer, the probability of a comparison involving Nazis or Hitler approaches 1” (Source: Wikipedia). Effectively, this means that the longer a discussion takes, the more likely it is that at least one of both parties in a discussion will use the Hitler-argument to compare the other side or their arguments to the horrors of Nazism.

It struck me that both sides in the religious debate did just that. But why both sides? Surely he can’t have been both religious and non-religious? Perhaps this had nothing to do with it? A bit of research (more Twitter) showed me that people nearly always ‘pulled a Godwin’ to affect the other emotionally. Emotional responds come after the reasonable arguments have been exhausted or are considered not worthy for use. And where reason ends, people become unreasonable. And the I saw the light! Okay, so it was my PC screen, but let’s not be pedantic, here. Here was my opportunity to do the following:

• Play my part in the Take That family.
• Provide the world with the revolutionary new insight that invoking Hitler or Nazism does not add to the discussion
• Realise that the above statement was very much redundant
• Provide a choice selection of tweets wherein people prove their lack of depth
• Destroy a desk or two by causing repetitive impacts between it and a forehead
• Respond with humour to some of the ‘better’ ones to underline the seriousness of the issue.

Let’s not kid ourselves. The issue is serious. Throughout history there have been many examples where people abandoned reason to pursue an emotional or spiritual cause. We need only to look a the horrors of the Second World War to see what happens when people stop being reasonable. But the way to tackle this issue is with aforementioned reason. And let’s be reasonable: what better way is there to make a point than to laugh and ridicule a statement or idea that is indeed laughable and ridiculous?